News
知的で柔軟なシステム計画技法の開発
本研究室では、従来の決定科学やシステム技法に加え、情報科学や知能工学を導入した知的意思決定支援技術、システム計画技法の開発を目指しています。
意思決定論や数理計画法、ファジィ理論、ラフ集合、計算論理学、アルゴリスム論、ゲーム理論などの基礎理論を研究するとともに、これらに基づいた新しい意思決定法、システム評価手法、モデリング、最適化手法、データ解析手法、社会システム技法、高速アルゴリスム、ソフトコンピューティングなどの開発と応用を行っています。
不確実情報の柔軟な取り扱いとシステム計画ヘの応用
意思決定が困難になる原因の一つとして、不確実性や曖昧さがあげられます。つまり、決定の結果得られる利得や決定(行動)に要する費用が正確かつ確実に推定できない場合や、複数の評価基準の存在などのため、判断基準が明確化できていない場合などです。また、人間による評価が言葉を介してなされるため、言葉に起因する曖昧さにも対処する必要があります。
これらの不確実性や曖昧さ、特に非確率的な不確実性に対処するため、ファジィ理論やラフ集合、Dempster-Shafer理論などの不確実性科学について研究するとともに、不確実性の下での意思決定法や数理計画法などへ応用しています。
たとえば、生産計画問題では、目的関数や制約条件の係数となる製品1個当たりの利益が100円と明確に与えられてきましたが、不良品の発生や売れ残りなどを考慮すれば現実には「だいたい100円」と不明確になる場合があります。また、多くの場合には制約条件となる機械の実働可能時間は「7時間まで」のように明確に与えられますが、残業などを考慮すれば、実際には「だいたい7時間まで」と柔軟に与えられる場合があります。このような係数の不明確さや制約の柔軟性をファジィ集合を用いて表現したファジィ数理計画問題の取り扱いと解法を研究しています。
一方、多基準意思決定問題と呼ばれる複数の評価基準のもとでの決定問題では、各評価基準と総合評価との関係を求めることは重要な課題です。この課題に対して、意思決定者の選好判断に関する多くの事例に基づき、各評価基準と総合評価との関係を決定ルールの形で抽出する方法を、ラフ集合に基づき研究して います。この課題には、医療診断や故障診断なども含まれ、医師や専門家が診断した多くの事例を用いて、診断知識を抽出することになります。ラフ集合に基づけば、決定に関与する必要最小限の評価基準や極小な条件をもつ決定ルールを求めることができます。また、ラフ集合を一般化して、問題設定に応じた決定ルールの抽出が可能となるこの他にも、曖昧な知識と不確実な情報から結論を導くファジイ推論法などを研究しています。
| Rice | Manure | Water | Evaluation |
|---|---|---|---|
| x1 | Very Large | Large | Good |
| x2 | Medium | Very Large | Good |
| x3 | Large | Large | Good |
| x4 | Very Small | Very Large | Good |
| x5 | Small | Large | Good |
| x6 | Medium | Medium | Good |
| x7 | Very Small | Large | Good |
| x8 | Very Large | Very Large | Bad |
| x9 | Large | Very Large | Bad |
| x10 | Very Large | Medium | Bad |
| x11 | Large | Small | Bad |
| x12 | Very Small | Large | Bad |
| x13 | Small | Small | Bad |
| x14 | Very Small | Very Small | Bad |
| Manure = VL, | Water = L | → Good |
| Manure = M | → Good | |
| Manure = L, | Water = L | → Good |
| Manure = VS, | Water = L | → Good |
| Manure = S, | Water = L | → Good |
| Manure = VL, | Water = VL | → Bad |
| Manure = L, | Water = VL | → Bad |
| Manure = VL, | Water = M | → Bad |
| Water = S | → Bad | |
| Water = VS | → Bad |
一般化したラフ集合によるルール抽出
| S | ≦ | Manure | ≦ | VL | → Good | |||||
| Manure | = | M | → Good | |||||||
| L | ≦ | Manure | ≦ | VL, | Water | = | VL | → Bad | ||
| L | ≦ | Manure | ≦ | VL, | S | ≦ | Water | ≦ | M | → Bad |
| VS | ≦ | Water | ≦ | S | → Bad |
組合せ最適化と離散アルゴリズム
社会システムや産業活動などに関係して現れる生産計画、環境計画、最適配送計画、スケジューリング、最適投資などを始めとする重要な問題の多くは、 大規模なシステムの最適化問題として捉えることができる。本研究課題では、これらのシステム最適化問題を解くための対象横断的な方法論を研究している。研 究対象は、工学諸問題だけでなく広く人間の諸活動全般に関わり、それらの最適化(効率化、高収益化、快適化、満足化、安定化、安全化など)を通して人類の福祉の向上に寄与したいと考えている。 具体的には、連続量に限らず離散変数や離散構造を有するシステム最適化問題の研究に従事している。これら諸問題を解決するため、まず第一に問題の本質を示す有効な離散構造の抽出、解析、および、それらに基づく高速なアルゴリズム開発という基礎理論の構築を行っている。次いで、得られた基礎理論を現実 に現れる問題に応用する。問題解決のための実用的な高速ソフトウェアの開発を行っている。 ここで扱う最適化問題は、上記からも分かるように、オぺレーションズ・リサーチ、数理計画の分野に限らず、人工知能データべース理論、分散システム、計算論理学などの多岐にわたっている。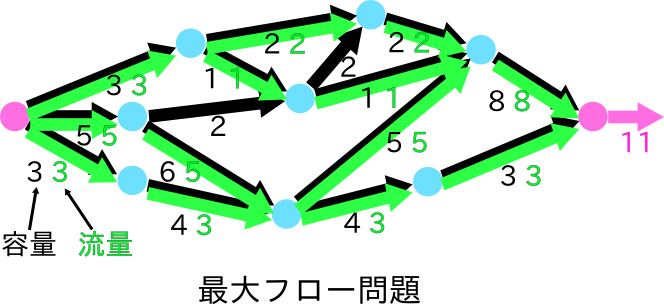 
具体的には、下記に示すような研究を行っている。
- グラフネットワークに関連する最適化問題
- 離散最適化理論とアルゴリスム理論
- 知識表現と推論問題
- 生産計画、スケジユーリング問題などの現実問題への応用
複数の意思決定者が競合・協調するときの意思決定法
経営戦略策定や公共施設建設などの意思決定状況では、競合あるいは協力関係にある他者の行動を適切に考慮すべき場合が多い。このときに有効なのゲーム理論である。
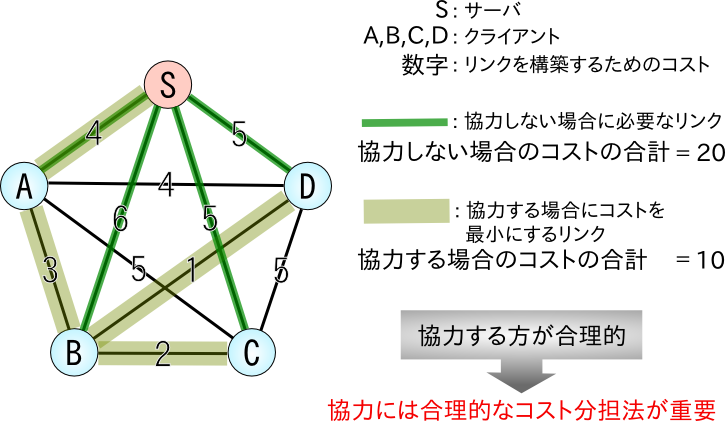
企業が生産活動を行う場合や、ネットワーク施設を構築する場合には、他者と協力することによって利益が増大できたり、コストを削減できたりする場合がある。このときには、すべての意思決定者が受け入れることができる利益配分やコスト分担の議論が重要である。本研究課題では、状況を適切に反映した利益 配分やコスト分担を議論する。また、この議論に基づいて企業間の契約に関する議論も行う。
たとえば、2名が2票ずつ投票権を持ち、1名が1票の投票権を持つときに多数決をする場合、この3名の発言力は同等と考えられる。このように、一般に投票によって意思決定を行う状況における投票者の発言力は、それそれが所有する票数に比例するとは限らない。このような発言力を測定する場合にもゲーム 理論が有効である。本研究課題では、投票者間の協力可能性の相違を考慮した各投票者の発言力の分析を行う。
この他、意思決定者が持っている資源の7割を提携に譲渡するというような協力関係が成立した場合の利益配分法、およひ将来の戦略の柔軟性を考慮した戦略の決定方法の研究も行う。
21459th visitor．
